Not sure where to start with this one, so I guess I will start at the beginning. First, a disclaimer: I am not afraid of reading above my weight class, and while I think I’ve bulked up a bit, there is still a ways I have to go before I will fully grasp all of Our Mathematical Universe. Don’t let that scare you off though – even though I know there are ideas I didn’t fully grasp, as well as ideas that I didn’t even notice were present, I still thoroughly enjoyed reading it. Besides, you are probably a lot smarter than I am.

This book made its way onto my to read pile courtesy of the Sam Harris podcast (aside: I am still struggling to determine if I am a Sam Harris Fan or Hater. I think I’m a bit of both). The book’s author, Max Tegmark, is a physics professor from MIT. Our Mathematical Universe is his attempt to make his ideas about the ultimate nature of reality accessible to the masses, in the tradition of those like Richard Feynman. His basic idea is this: reality is math. No, not that reality is described by math, but at it’s core actually IS math. Unites, featureless. Just quantity and relationship.
While that may seem like a pretty straightforward (if potentially hard to believe) claim, it has some pretty hard to grasp consequences, specifically that we exist within a four level multiverse. I’m not going to cover all the details of the four different levels, but merely comment that level 1 was pretty easy for me to grasp. Level 2 I think I almost understand. Level 3 lost me. And I think I get level 4 too – but I have doubts.
What fascinated me most about this book is the connections I found with topics ranging far beyond cosmology and particle physics. If I worked at Half Price Books and Our Mathematical Universe was on my cart to be shelved, I could just as easily put it in the Philosophy section (or even Buddhism) section as the Physics section. This is not to say that the book isn’t scientific. As Dr. Tegmark points out, quite rightly, for a theory to be scientific, you don’t have to be able to test all of its predictions, only some of them. Rather, the ideas he touches on sound similar to those I’ve been reading in those other areas.
Take for instance the ideas about the perception of time passing that comes in the chapter talking about the relationship between physical reality and mathematical reality:
Subjective perceptions of duration and change are qualia, basic instantaneous perceptions, just as reddened, blueness or sweetness.
Compare that to this quote from Zen Buddhist master Ch’an Master Hui-neng, writing in the 7th century:
In this moment there is nothing that comes to be. In this moment there is nothing that ceases to be. Thus there is no birth-and-death to be brought to an end. Thus the absolute peace in this present moment. Though it is at this moment, there is no limit to this moment, and herein lies eternal delight.
Or the discussion of self concept:
I’m arguing that your perceptions of having a self, that subjective vantage point you call “I”, are qualia just as your subjective perceptions of “red” and “green” are. In short, redness and self-awareness are both qualia.
Sounds like the same idea as Anatta to me.
I also found some interesting implications for my objectivist friends:
If you believe in an external reality independent of humans, then you must also believe that our physical reality is a mathematical structure (emphasis added)
Looks like the Randians need to study up on their math ;-).
There are a few other ideas that were new to me, but also struck me as deeply insightful in a philosophical sense. For example in a discussion about the level 4 multiverse, Dr. Tegmark draws a few conclusions from the idea that we live inside a mathematical structure that seem profound (to me anyway).
First an interesting idea coming from a math and physics guy:
Infinity is a convenient assumption, but not part of reality.
He goes on to explain that infinity helps us solve a certain class of math problems, but just like Newton’s laws of motion are only useful on objects of a particular scale, the assumption that there is an infinity sub dividable space may just be a “convenient” stand in, for lots and lots of granular space that is too hard for us to measure and count.
Then a few ideas about “initial conditions” which come from some discussion about the permanence of mathematical structure and the concept of space time being fixed and unchanging:
Initial conditions aren’t about our physical reality, but about our place in it.
and:
Although we though all this information (referring to initial conditions) was about our physical reality, it was about us.
and finally:
Apparent arbitrary initial conditions are caused by multiple universes, apparent randomness is caused by multiple you’s.
Ponderous, man, really ponderous. Seriously, I’m not sure what to take from these specific ideas, but they strike me as being really important to understanding my place in the universe and perhaps provide an alternative perspective to the things that happen to me in daily life. More meditation and processing is required.
The last idea that jumped out comes later in the chapter on the level 4 multiverse. He writes that there are 3 basic mathematical concepts with well defined relationships: formal systems, computations and mathematical structures. He goes on to wonder if there is something even more fundamental at the base of these three ideas that we have yet to discover. For whatever reason, this made me wonder if that is something we can actually understand?
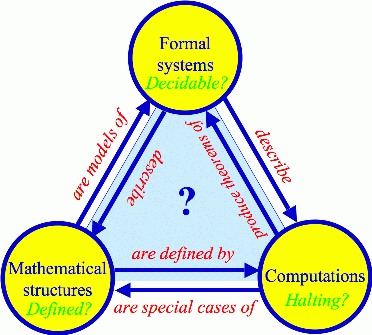
Let me explain. In Sapiens (which it just occurred to me that I never did a review of here….thought I was caught up after this one…sigh…), Harari argues that the thing that makes humans unique/powerful when compared to all other animal species is our storytelling ability: our ability to create myth, fiction, and story and to communicate it to others. Some have taken this further and claimed that our internal reality is only understood in the context of narrative. No, this isn’t “tell a story and it’s true”, but rather the idea that the only way our brains can actually comprehend anything is through story. If this is the case, then I wonder the core beneath formal systems, computations and mathematical structure is so abstract, so absent narrative, that humans are unable to understand it? This seems similar to the idea of the Tao: if you can talk about it, it’s no longer the Tao ;-).
In the end, I am really glad I heard about this book, bought it and read it. While I’m sure there is knowledge I am leaving behind in its pages, it has opened up and connected some ideas for me that were previously disorganized. If you feel like stretching a bit, or are more of a Physics and Math Zen Master, then I highly recommend it.
Leave a Reply